目录
快速导航-
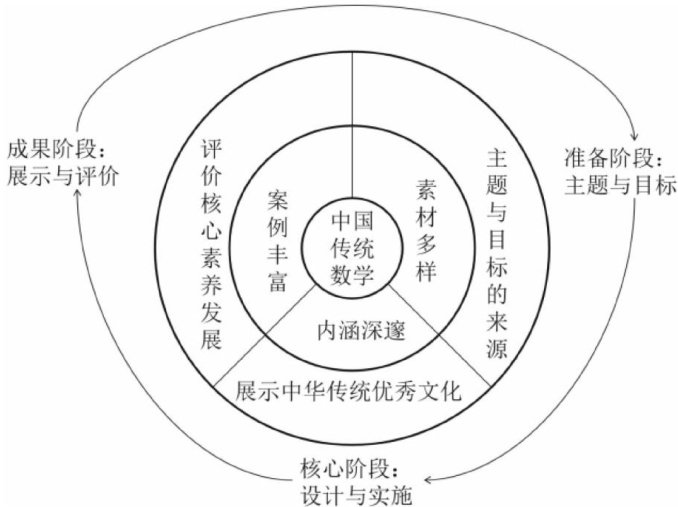
教学纵横 | 中国传统数学融入跨学科项目化学习的价值、原则和策略
教学纵横 | 中国传统数学融入跨学科项目化学习的价值、原则和策略
-
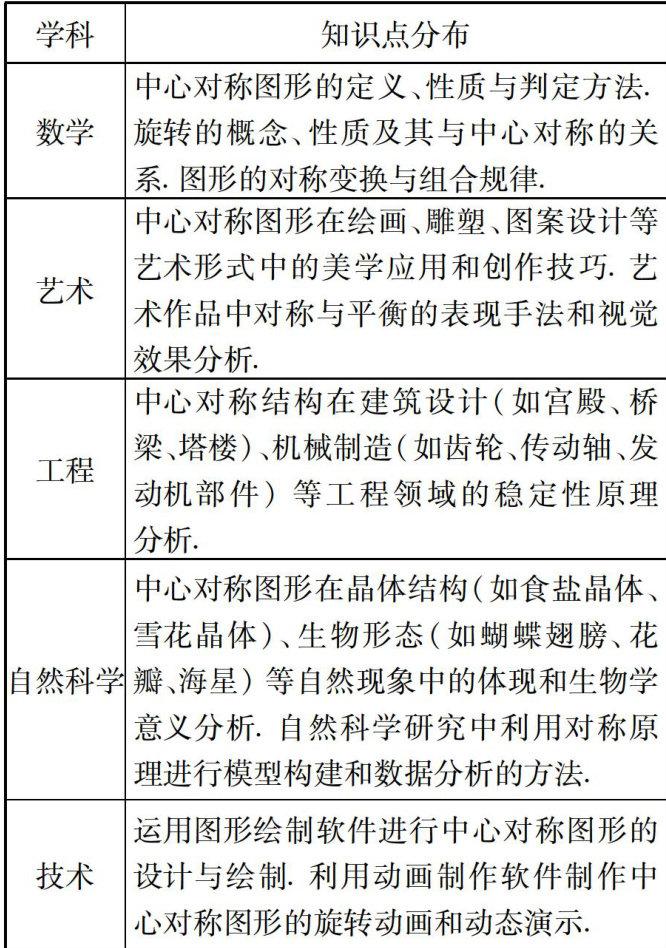
教学纵横 | 基于STEAM理念的跨学科视域探寻生活中的数学之美
教学纵横 | 基于STEAM理念的跨学科视域探寻生活中的数学之美
-
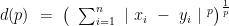
教学纵横 | 新定义试题中“距离”的可视化探究
教学纵横 | 新定义试题中“距离”的可视化探究
-
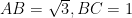
教学纵横 | 聚焦思维进阶的初高中数学衔接设计研究
教学纵横 | 聚焦思维进阶的初高中数学衔接设计研究
-
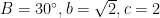
教例探微 | 深挖教材对话功能 合理衍生教学思考
教例探微 | 深挖教材对话功能 合理衍生教学思考
-
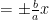
教例探微 | 提出真问题促进真探究实现真理解
教例探微 | 提出真问题促进真探究实现真理解
-
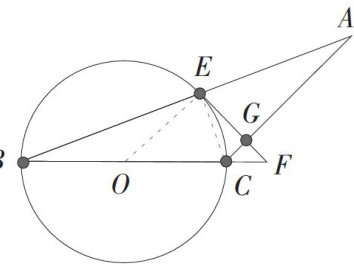
教例探微 | 以平面几何教学为例,培养学生逻辑思维能力
教例探微 | 以平面几何教学为例,培养学生逻辑思维能力
-
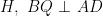
教例探微 | 研发一题一课,提升压轴题解题教学品质
教例探微 | 研发一题一课,提升压轴题解题教学品质
-
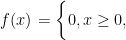
聚焦高考 | 2025年高考数学上海卷第12题的解法探究与推广
聚焦高考 | 2025年高考数学上海卷第12题的解法探究与推广
-
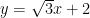
聚焦高考 | 借助数形结合,求解高考试题
聚焦高考 | 借助数形结合,求解高考试题
-
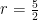
聚焦高考 | 空间向量法在2025年高考立体几何中的应用
聚焦高考 | 空间向量法在2025年高考立体几何中的应用
-
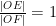
聚焦高考 | 一道双曲线中两线段比值为定值试题的探究
聚焦高考 | 一道双曲线中两线段比值为定值试题的探究
-
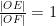
聚焦高考 | 一道定点在动直线上的联考题探究
聚焦高考 | 一道定点在动直线上的联考题探究
-
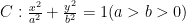
初数研究 | 一个经典不等式引发的探究
初数研究 | 一个经典不等式引发的探究
-
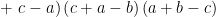
初数研究 | 与三角恒等式相关的不等式新探
初数研究 | 与三角恒等式相关的不等式新探
-
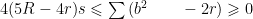
初数研究 | 《数学通讯》问题699的证明、逆向及类似
初数研究 | 《数学通讯》问题699的证明、逆向及类似
-
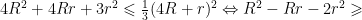
初数研究 | 三角形的四心相伴三角形的若干不等式链
初数研究 | 三角形的四心相伴三角形的若干不等式链
-
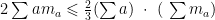
解题方法与技巧 | 一道以有界性为背景的数列问题的解法探究
解题方法与技巧 | 一道以有界性为背景的数列问题的解法探究
-
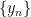
解题方法与技巧 | 一道函数与对数综合题的多维度探究
解题方法与技巧 | 一道函数与对数综合题的多维度探究
-
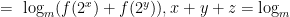
解题方法与技巧 | 一道圆锥曲线试题的求解与推广
解题方法与技巧 | 一道圆锥曲线试题的求解与推广
-
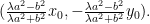
解题方法与技巧 | 逻辑推理素养导向下的三种不同水平试题示例
解题方法与技巧 | 逻辑推理素养导向下的三种不同水平试题示例
-
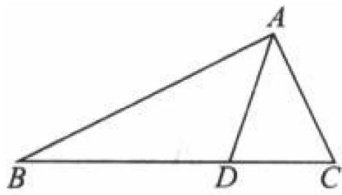
解题方法与技巧 | 几道典型三角形问题的多解探析
解题方法与技巧 | 几道典型三角形问题的多解探析
-
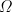
竞赛之窗 | 一道2023年高联预赛平面几何题的探究推广
竞赛之窗 | 一道2023年高联预赛平面几何题的探究推广























 登录
登录